Augenspiele

 

Täuschungen/ Rätsel/ Wunder

    

Wie sich unsere Augen  täuschen lassen:

Die waagerechten Linien sind parallel !!!

Man denkt, es ist eine Spirale,

 aber es sind Kreise !

Schau auf den Mittelpunkt und bewege

Deinen Kopf zum Bild und zurück.

Was siehst Du ?

Erstaunlich oder ???

Sieht die Dame in 70 Jahren vielleicht so aus???

Man glaubt es nicht, aber man sieht es doch !!!

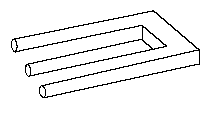
Eine tolle unmögliche Figur !

Ist das nicht endgeil das Teil?

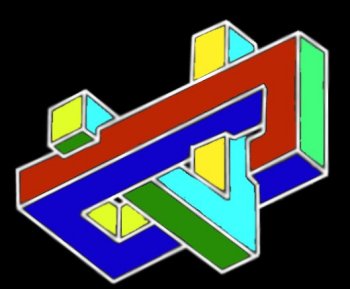
Beide Leute gehen in die gleiche Richtung,

aber einer nach oben und der andere nach unten  - 

 geil oder ???

Na, wieviel Säulen siehst Du ???

Die scheinbar krummen Linien sind aber gerade !!!

Ist doch schon sehr rätselhaft oder?

 

Man geht hier nur die Treppe hoch -

wie geht sowas???

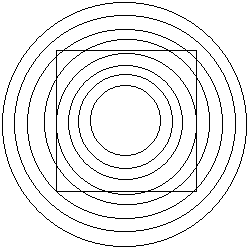
Das ist ein ganz normales Quadrat !!!

Hier ist nichts krumm oder schief -

alles ist exakt viereckig

und die Linien somit parallel  !!!

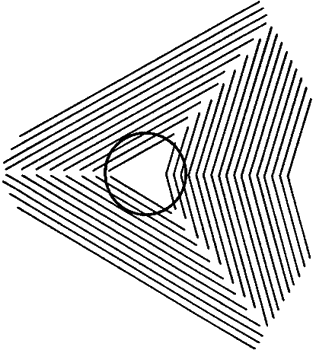
Nixda, das ist    k e i n    Oval ,  

 sondern ein ganz normaler Kreis !!!

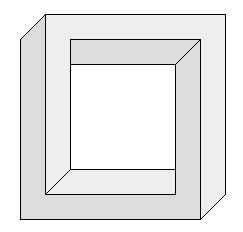
Diese Figur bau mal bitte nach oder geht das nicht?

Auch diese Diagonalen sind natürlich parallel !!!

Schau genau hin, was Du alles sehen kannst -

wie ein Wunder oder ?

Zu dieser Rätselfigur muss ich nix sagen oder ???

Welches blaue Teil ist größer?

Keins, denn sie sind gleichgroß!!!

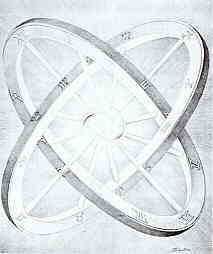
Das ist wieder so ein erstaunliches Gebilde !

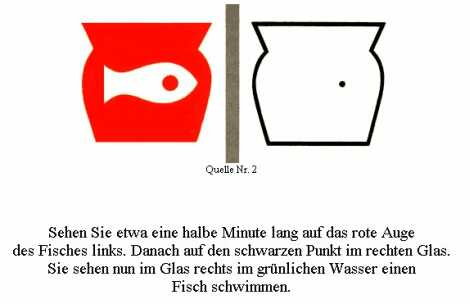
Siehst Du eine Vase oder zwei Gesichter ?

 Ist schon geil das Teil oder ?

Na, welche Figur ist grösser ?  

 Natürlich sind sie gleichgross !!!

 

Und? Bewegen sich die Kreise???

Natürlich  nicht !!!

Es sind keine Kreise oder Punkte vorhanden  - 

 alles Täuschung !!!

Wenn das wer weiss,

kann er mir ja eine eMail schicken,

ich lob den dann, wenns richtig ist !!!

Interessant oder ???

Man kann sowas kaum fassen oder???

Hm, arbeiten die Leute am Fussboden oder

an der Decke ???

Siehst Du, falsch getippt !!  

Die sind nämlich gleich gross !!!

Welches Dach gehört denn nun zu

welchem Haus???

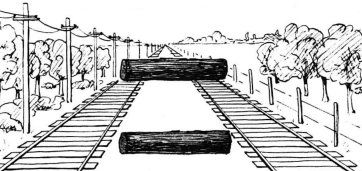
Und welcher Baumstamm ist nun größer und schwerer? 

Keiner, sie sind gleichgroß!!!

Mein tolles Rätsel:

Die Dreiecke sind gleichgross, das kann man prüfen, oder?

Poste mir die Lösung und Du darfst den Titel

" Schlauer Pfucks "

tragen !!!*grins*

Und jetzt kommt noch der Megahammer !

Schau  20 Sekunden auf die vier  kleinen

übereinanderliegenden Punkte

in der Mitte des Bildes  - 

dann an eine helle Wand Deines Zimmers

oder an die Decke ! 

Du siehst dann eine echte   E r s c h e i n u n g   !!!

 

 

 

 

 

Lösung

des Rätsels zum " Schlauen  Pfucks "

Das große Dreieck ist in Wirklichkeit ein Viereck.

Rechnerische Lösung:
Denn die Hypothenuse hat einen Knick und

zwar einmal nach innen und einmal nach außen,

jeweils dort, wo die kleinen Dreiecke aufeinanderstoßen.

Das kann man sehen,

 wenn man an der Hypothenuse entlangschaut.

Etwas analytischer:
Erstmal eine kleine Flächenbetrachtung:
- orangene Flächen: 7 Einheiten
- hellgrüne Flächen: 8 E
- rotes Dreieck: (8x3)/2 = 12 E
- grünes Dreieck: (2x5)/2 = 5 E
macht zusammen: 7+8+12+5 = 32 E
großes Dreieck: (13x5)/2 = 32,5 E
Da kann doch was nicht stimmen...

Da sich die Größen der 4 Flächen tatsächlich nicht ändern,

muß wohl die 32,5 falsch sein. Andererseits

ist die Flächenberechnung für das große Dreieck korrekt.

Also ist offensichtlich die Annahme falsch,

daß die große Fläche ein Dreieck ist.

Eine mögliche Bestätigung dieser These geht über

die Winkel der beiden Dreiecke: Seien a und b die

Winkel unten links des roten resp. grünen Dreiecks.

Dann gilt: - tan(a)=3/8=1/2,66666 und tan(b)=2/5=1/2,5

Also tan(a) ungleich tan(b) und daher a ungleich b.
Wenn aber a ungleich b,

 dann hat die vermeintliche Hypothenuse den o. g. Knick

und die große Fläche ist kein Dreieck.

Die obere Fläche hat 32 E und die unteren Fläche 33 E.

Grafische Lösung:

Jedem Löser dieses Rätsel wird der Titel

 s c h l a u e r   P f u c k s 

zugeschickt!

Dieser Titel  steht noch über dem Nobelpreis !!!